La Integral
Técnica y Método
1.8. Integración por partes
Este método es útil cuando se tiene el producto de dos funciones. La fórmula para
integración por partes es:
Esta fórmula se deduce de la diferencial del producto de dos funciones.
Despejando 
Al integra la expresión, se obtiene dicha fórmula.
Esta fórmula permite expresar la integral original en términos de otra más fácil de integrar,
dependiendo de la manera en que se seleccione 
. Dado que es fundamental escoger
estas partes de la integral original, se sugiere para su elección:
a) Determinar la parte del integrando 
tal que al derivarla resulte una función más sencilla que 
.
El resto del integrando se tomará como 
.
b) Determinar como 
la parte del integrando que sea más complicada y que se pueda integrar,
así el resto del integrando se tomará como 
.
Para los siguientes casos se utiliza esta técnica de integración por partes:
(Algebraicas) por (trigonométricas)
(Algebraicas) por (exponenciales)
(Algebraicas) por (logarítmicas)
(Exponenciales) por (trigonométricas)
Logarítmicas
Trigonométricas inversas
(Algebraicas) por (trigonométricas inversas)
Veamos algunos ejemplos:
1. 
Sustituyendo en la fórmula
Por lo tanto:
2. 
Sustituyendo en la fórmula
Por lo tanto:
3. 
Aplicando la fórmula
Por lo tanto:
4. 
Aplicando fórmula
Por lo tanto:
5. 
Aplicando fórmula
Ahora aplicar un cambio de variable para la nueva integral
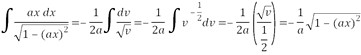
Así:
6. 
Aplicando la fórmula
Obtengamos la nueva integral, para ello, se realiza la división:
Por lo tanto:
7. 
Así:
La nueva integral tiene que resolverse nuevamente por partes, así que:
Por lo que
Sustituyendo
Despejando 
se obtiene que:
Finalmente:
8. 
9. 
Primeramente se descompone la integral de la siguiente manera:
Finalmente:
10. 
Descomponer la integral de la siguiente manera:
Para obtener 
la integral se resuelve haciendo un cambio de variable:
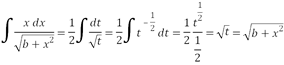
Sustituyendo en la fórmula
Esta última integral se resuelve aplicando nuevamente cambio de variable
Finalmente:
Autores:
Eduardo Ochoa Hernández
Nicolás Zamudio Hernández
Lizbeth Guadalupe Villalon Magallan
Mónica Rico Reyes
Pedro Gallegos Facio
Gerardo Sánchez Fernández
Rogelio Ochoa Barragán