La Integral
Técnica y Método
1.6. Integración completando el cuadrado
Existen integrales que contienen en el denominador un trinomio de la forma ![]()
el cual puede transformarse a binomios de la forma:
![]()
Para ello se utiliza el método de completar un TCP y así aplicar las fórmulas básicas de
la (19), a la (23). Ilustremos el procedimiento con algunos ejemplos.
31. ![]()
Se completa el TCP del denominador
![]()
![]()
Entonces
![]()
Así la integral se expresa como sigue
![]()
Por lo que podemos aplicar la fórmula (19), haciendo:
![]()
![]()
![]()
32. ![]()
Completando el TCP
![]()
Así que, aplicando (20)
![]()
![]()
33. ![]()
Completar el TCP
![]()
![]()
![]()
Así que la integral se expresa como sigue:
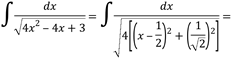
Aplicar (23)
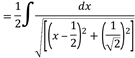
![]()
Este resultado se puede simplificar de la siguiente manera:
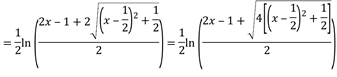
![]()
![]()
Finalmente se expresa el resultado con una sola constante:
![]()
34. ![]()
Completando el TCP
![]()
Aplicando (25)
![]()
![]()
![]()
![]()
![]()
Finalmente
![]()
35. ![]()
Completando el TCP del denominador
![]()
![]()
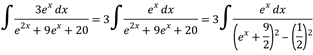
Aplicando (20)
![]()
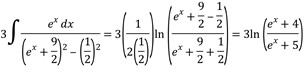
Finalmente:
![]()
36. ![]()
Completando el TCP
![]()
Aplicando (24)
![]()
![]()
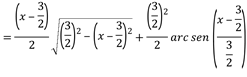
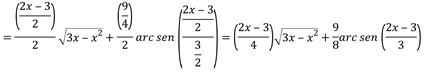
Finalmente:
![]()
Autores:
Eduardo Ochoa Hernández
Nicolás Zamudio Hernández
Lizbeth Guadalupe Villalon Magallan
Mónica Rico Reyes
Pedro Gallegos Facio
Gerardo Sánchez Fernández
Rogelio Ochoa Barragán