La Integral
Técnica y Método
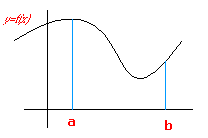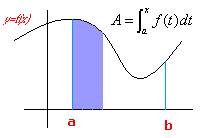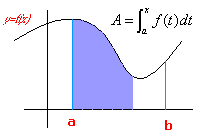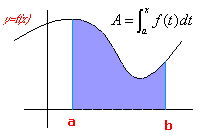
Ejercicios resueltos de técnicas de integración
1.-![]()
Solución:
Para la función ![]() , sustituimos
, sustituimos ![]() , y
, y ![]()
![]()
para la integral ![]() , la dividamos:
, la dividamos:
![]()
Las integral la resolvemos como sumas de integrales:
![]()
Para la integral ![]() , substituimos s=u+9 y ds=du:
, substituimos s=u+9 y ds=du:
![]()
Integramos ![]() como log(s):
como log(s):
![]()
La integral de la contante:
![]()
Sustituimos para s=u+9:
![]()
Substituimos para ![]() :
:
![]()
Por tanto la solución es:
![]()
2.![]()
Solución:
Para la integral ![]() , subtituimos
, subtituimos ![]() , y
, y ![]() :
:
![]()
Pala integral de ![]() , es
, es ![]() :
:
![]()
Sustituyendo ![]() , por tanto la solución es:
, por tanto la solución es:
![]()
3.![]()
Solución:
Para la función ![]() , subtituimos u=x+1 y du=dx:
, subtituimos u=x+1 y du=dx:
![]()
Para integrar ![]() , substituimos
, substituimos ![]() , y
, y ![]() :
:
![]()
Para integrar ![]() , se hara por partes,
, se hara por partes, ![]() , por tanto:
, por tanto:
![]()
![]()
Integrando ![]() :
:
![]()
Sustituyendo ![]() :
:
![]()
Sustituyendo u=x+1:
![]()
por tanto la solución es:
![]()
![]()
Sustituyendo
![]()
Entonces
![]()
Multiplicando numerador y denominador de sec(u) por tan(u) +sec(u)
![]()
Entonces
![]()
ahora sustituyendo s
![]()
tenemos sustituyendo u tenemos
![]()
![]()
Sustituyendo
![]()
entonces tenemos
![]()
escribiendo
![]()
entonces
![]()
integrando la suma termino a termino
![]()
sustituyendo en la primer integral
![]()
entonces
![]()
sustituyendo (s) y (u)
![]()
![]()
Haciendo división larga
![]()
Sacando el factor 4 desde el denominador
![]()
Para la segunda integral sustituir
![]()
Entonces
![]()
Integrando
![]()
![]()
Al separar la fracción
![]()
Integrando
![]()
![]()
Usando fracciones parciales
![]()
Integrando la suma termino a término y sacando factores
![]()
Para la primer integral sustituir
![]()
y para la tercera integral sustituir
![]()
![]()
ahora integrando
![]()
Sustituyendo (u) y (s)
![]()
![]()
Separando la fracción y sacando los factores
![]()
Para la primer integral sustituir
![]()
y sacando el factor 4 de la segunda integral
![]()
Entonces sustituir para la segunda integral
![]()
Obtenemos
![]()
Integrando
![]()
Sustituyendo (u) y (s)
![]()
![]()
Sustituyendo
![]()
Entonces
![]()
factorizando el denominador
![]()
haciendo división larga
![]()
integrando a la suma termino a termino
![]()
reescribiendo
![]()
Entonces
![]()
integrando a la suma termino a término y sacando factores
![]()
para la primer integral sustituir
![]()
entonces
![]()
Para la segunda integral completar el cuadrado
![]()
Sustituir
![]()
entonces
![]()
Sacando el factor 27/4 del denominador
![]()
Sacando los factores constantes
![]()
Sustituyendo
![]()
Entonces
![]()
integrando
![]()
para la tercer integral sustituir
![]()
entonces
![]()
integrando lo restante+C
![]()
sustituyendo (u), (v), (w), (p)
![]()
![]()
Sustituir
![]()
Entonces
![]()
integrando
![]()
sustituyendo (u)
![]()
![]()
Integrando por partes donde
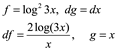
Entonces
![]()
Nuevamente integrando por partes donde
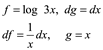
Entonces
![]()
![]()
Integrando por partes donde
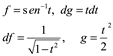
entonces
![]()
Para la integral sustituir
![]()
entonces
![]()
Escribir ![]() como
como![]() entonces
entonces
![]()
Integrando la suma parte por parte
![]()
integrando
![]()
sustituyendo (u) donde
![]()
![]()
![]()
![]()
Expandiendo la integral multiplicando tenemos
![]()
Integrando la suma termino a término y sacando factores constantes
![]()
Integrando
![]()
![]()
Usando fracciones parciales tenemos
![]()
Integrando la suma termino a termino
![]()
Integrando usando cambio de variable
![]()
![]()
Integrando por partes donde
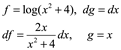
Entonces
![]()
Haciendo división larga se tiene
![]()
Sacando el factor 4 del denominador
![]()
Sustituir
![]()
entonces
![]()
integrando
![]()
sustituyendo (u)
![]()
![]()
Sustituir
![]()
Entonces
![]()
sustituyendo (u)
![]()
![]()
Usando fracciones parciales tenemos:
![]()
Sacando constantes integrando termino a termino
![]()
Para las ultimas 2 integrales usar el cambio de variable donde
![]()
obteniendo
![]()
integrando
![]()
sustituyendo (u)
![]()
![]()
Completando el cuadrado
![]()
Sustituir
![]()
entonces
![]()
Sustituir ![]()
entonces
![]()
Sustituyendo (u) y (s) tenemos
![]()
![]()
Cancelando términos comunes en numerador y denominador
![]()
Usando fracciones parciales tenemos:
![]()
Integrando la suma termino a termino y sacando factores constantes
![]()
Para las primeras dos integrales usar el cambio de variable donde
![]()
y para la ultima integral utilizar el cambio de variable donde
![]()
Entonces
![]()
integrando
![]()
Sustituyendo (s) y (u)
simplificando
![]()
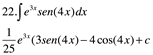
![]()
Escribir
![]()
entonces
![]()
Integrando
![]()
![]()
Usando la identidad
![]()
entonces
![]()
sustituir
![]()
entonces
![]()
Sustituir
![]()
entonces
![]()
sustituyendo (s) y (u)
![]()
![]()
Usar la identidad trigonométrica
![]()
entonces
![]()
Sustituir
![]()
entonces
![]()
Sustituyendo (u)
![]()
![]()
Tomar la integral
![]()
luego integrar por partes
Donde
![]()
entonces
![]()
Multiplicar denominador y numerador de la integral por
![]()
Entonces
![]()
Sustituir
![]()
Integrar
![]()
Sustituyendo (u)
![]()
![]()
Integrar por partes donde
![]()
Entonces
![]()
![]()
Sustituir
![]()
entonces
![]()
Sustituyendo (u)
![]()
![]()
Usar la identidad trigonométrica
![]()
Entonces
![]()
Sustituir
![]()
Entonces
![]()
Integrando
![]()
sustituyendo (u)
![]()
![]()
Tomar la integral
![]()
usar la identidad trigonométrica
![]()
Entonces
![]()
Reescribir la primera integral en términos de seno y coseno
![]()
Sustituir
![]()
entonces
![]()
Para la segunda integral multiplicar denominador y numerador por
![]()
Entonces
![]()
sustituir
![]()
entonces
sustituyendo (u) y (s)
![]()
![]()
Sustituir ![]() entonces
entonces
![]()
Sustituir
![]()
Entonces
![]()
sustituyendo (s) y (u)
![]()
![]()
Expandiendo la integral tenemos
![]()
para la primera integral
Hacer por partes donde
![]()
entonces
![]()
Las dos integrales restantes son iguales pero de diferente signo por lo
tanto se cancelan
Dando como resultado
![]()
![]()
Sustituir
![]()
entonces
![]()
Usando la fórmula de reducción resulta
![]()
ahora reescribimos la cot en términos de sen y cos entonces
![]()
sustituir
![]()
Entonces
![]()
Sustituyendo (s) y (u)
![]()
![]()
Expandiendo la integral
![]()
Integrando
![]()
![]()
Cambiar todo a sen y cos
![]()
Sustituir
![]()
lo que nos produce un límite inferior
![]()
Y un nuevo límite superior
![]()
Entonces
![]()
Multiplicamos el orden de los limites de integración ya que el inferior es
mayor que el superior, entonces multiplicamos por -1 ,
Tenemos
![]()
Integrando
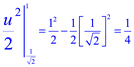
![]()
No aparece con pasos intermedios así que la solución a la integral indefinida es
![]()
y el resultado a la integral definida es:
![]()
![]()
Sustituir
![]()
luego transformamos la integral usando las sustituciones
![]()
Entonces
![]()
Simplificando
![]()
Cancelando términos comunes
![]()
usando fracciones parciales
![]()
Integrando
![]()
sustituyendo (u)
![]()
![]()
Aplicando fracciones parciales
![]()
Realizar el cambio de variable simple para cada integral y evaluar los nuevos limites donde
![]()
entonces
![]()
Integrando
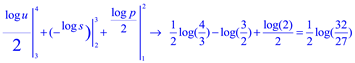
![]()
Aplicando fracciones parciales
![]()
Realizar el cambio de variable simple para cada integral y evaluar los nuevos limites donde
![]()
entonces
![]()
Integrando
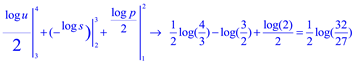
![]()
Sustituir
![]()
Entonces
![]()
Sustituir
![]()
entonces
![]()
Haciendo división larga
![]()
Hacer cambio de variable simple para integrar entonces
![]()
Regresando a términos de x
![]()
Evaluando los limites da ![]()
![]()
Hacer por partes donde
![]()
Entonces
![]()
Nuevamente integramos por partes donde
![]()
entonces
![]()
la integral restante es idéntica a la original entonces las pasamos al mismo lado
![]()
finalmente despejando
![]()
![]()
Sustituir
![]()
Entonces
![]()
integrando:
![]()
sustituyendo (u)
![]()
![]()
Sustituir
![]()
Entonces
![]()
para resolver esta integral usar la formula
![]()
En este caso los coeficientes de u son 1 entonces sustituyendo (u)
![]()
![]()
Sustituir
![]()
entonces
![]()
Integrar por partes donde
![]()
entonces
![]()
Integrando:
![]()
![]()
Sustituyendo
![]()
Entonces
![]()
Integrando por partes donde:
![]()
Entonces
![]()
sustituyendo (u)
![]()
![]()
Sustituyendo
![]()
entonces s
![]()
ustituyendo (u)
![]()
![]()
Usando la identidad trigonométrica donde
![]()
entonces
![]()
sustituir
![]()
entonces
![]()
integrando:
![]()
sustituyendo (u)
![]()
![]()
Escribir
![]()
y
![]()
Entonces
![]()
Sustituir
![]()
entonces
![]()
sustituyendo (u)
![]()
![]()
Completando el cuadrado
![]()
sustituir
![]()
Entonces
![]()
hacer el cambio trigonométrico
![]()
entonces
![]()
usando la fórmula de reducción para la secante obtenemos
![]()
integrando la ultima integral
![]()
Sustituyendo (s) y (u)
![]()
![]()
Completar el cuadrado
![]()
sustituir
![]()
Entonces
![]()
realizar el cambio trigonométrico
![]()
entonces
![]()
Integrando:
![]()
sustituyendo (s)
![]()
![]()
Usar la identidad trigonométrica
![]()
entonces
![]()
sustituir
![]()
entonces
![]()
integrando:
![]()
sustituyendo (u)
![]()
![]()
Sustituir
![]()
entonces
![]()
usando la fórmula de reducción para el coseno:
![]()
para la integral restante escribir
![]()
entonces
![]()
expandiendo la integral
![]()
haciendo un cambio de variable
Donde
![]()
entonces
![]()
Integrando:
![]()
sustituyendo (u) y (s)
![]()
![]()
Sustituir
![]()
entonces
![]()
haciendo división larga
![]()
integrar y para la integral fraccionaria sustituir
![]()
entonces
![]()
Sustituyendo (u) y (s)
![]()
![]()
no muestra pasos intermedios
![]()
Aplicando fracciones parciales
![]()
Para la primer integral hacer el cambio
![]()
entonces
![]()
para la segunda integral nos da igual a
![]()
entonces
![]()
ahora hacemos el cambio de variable
![]()
entonces
![]()
integrando
![]()
ustituyendo(u) y (s)
![]()
![]()
Sustituir
![]()
Entonces
![]()
usar la identidad trigonométrica
![]()
Entonces
![]()
Multiplicar la primera integral por tan u +sec u (numerador y denominador)
![]()
Sustituir
![]()
Entonces
![]()
integrando
![]()
sustituyendo (u) y (s)
![]()
![]()
Usar la identidad trigonometrica
![]()
Entonces
![]()
para la primer integral integrar por partes donde
![]()
entonces
![]()
sustituir
![]()
entonces
![]()
integrando
![]()
sustituyendo (u)
![]()
![]()
Expandiendo la integral
![]()
hacer por partes donde
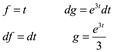
entonces
![]()
integrando por partes donde
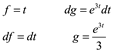
entonces
![]()
integrando
![]()
![]()
Reescribir la integral como
![]()
Sustituir
![]()
entonces
![]()
Integrando por partes donde:
![]()
entonces
![]()
Integrando
![]()
sustituyendo (u)
![]()
![]()
Sustituir
![]()
entonces
![]()
usando la identidad trigonometrica
![]()
tenemos
![]()
Integrando
![]()
sustituyendo (u)
![]()
![]()
Sustituir
![]()
entonces
![]()
Integrando
![]()
sustituyendo (u)
![]()
entonces el resultado es
![]()
![]()
Sustituir
![]()
luego transformar la integral usando las
sustituciones
![]()
Entonces
![]()
simplificando
![]()
completando el cuadrado
![]()
sustituir
![]()
Entonces
![]()
sacando el factor fuera del denominador
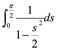
sustituir
![]()
entonces
![]()
integrando
![]()
regresando a términos de (x)
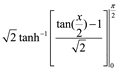
obteniendo como resultado
![]()
![]()
Integrando por Partes donde:
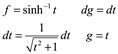
Entonces
![]()
Sustituir
![]()
entonces
![]()
Integrando
![]()
sustituyendo (u)
![]()
![]()
solución no disponible en wólfram
![]()
![]()
Sustituir
![]()
entonces
![]()
sustituir
![]()
Entonces
![]()
sacando el factor -1 del denominador
![]()
Integrando
![]()
regresando a términos de x
![]()
lo que da como resultado
![]()
![]()
Rescribir la integral como:
![]()
Sustituir para la primera integral
![]()
entonces
![]()
para la segunda integral completar el cuadrado
![]()
sustituir
![]()
entonces
![]()
integrando
![]()
sustituyendo (u) y (s)
![]()
![]()
Tomar la integral
![]()
sustituir
![]()
Entonces
![]()
usar la identidad trigonométrica
![]()
Entonces
![]()
sustituir
![]()
Entonces
![]()
Expandiendo
![]()
integrando
![]()
regresando a términos originales
![]()
![]()
Sustituir
![]()
entonces
![]()
usar la identidad trigonométrica
![]()
Entonces
![]()
sustituir
![]()
entonces
![]()
Integrando
![]()
regresando a términos originales
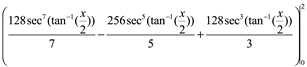
entonces esto da como resultado
![]()
![]()
Tomar la integral
![]()
Pasar a sen y cos la primer integral
![]()
Sustituir
![]()
entonces
![]()
Integrando
![]()
sustituyendo (u)
![]()
![]()
Tomando en cuenta la identidad
![]()
Sustituir
![]()
entonces
![]()
Integrando
![]()
sustituyendo (u)
![]()
![]()
Expandiendo la integral tenemos
![]()
La primer integral la hacemos por partes donde
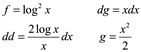
Entonces
![]()
Haciendo la segunda integral por partes donde
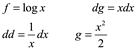
Entonces
![]()
finalmente
![]()
![]()
Usando la identidad trigonométrica
![]()
Entonces
![]()
Expandiendo la integral tenemos
![]()
integrando por partes donde
![]()
entonces
![]()
sustituir
![]()
entonces
![]()
integrando
![]()
sustituyendo (u)
![]()
![]()
Tomar la integral
![]()
sustituir
![]()
entonces
![]()
Integrando
![]()
sustituyendo
![]()
![]()
Racionalizando la integral
![]()
Entonces
![]()
sustituir
![]()
Entonces
![]()
integrando
![]()
sustituyendo (u)
![]()
![]()
Usando la identidad trigonométrica
![]()
Entonces
![]()
Sustituir
![]()
entonces
![]()
Integrando
![]()
sustituyendo (u)
![]()
![]()
Sustituir
![]()
entonces
![]()
sustituir
![]()
Entonces
![]()
usando fracciones parciales
![]()
Expandiendo la integral
![]()
sustituir
![]()
entonces
![]()
Integrando
![]()
regresando a términos de (t)
![]()
simplificando
![]()
![]()
Sustituir
![]()
entonces
![]()
integrando
![]()
Sustituyendo (u)
![]()
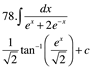
![]()
Sustituir
![]()
entonces
![]()
integrando por partes
![]()
entonces
![]()
sustituyendo (u)
![]()
![]()
Integrar por partes donde
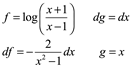
entonces
![]()
Sustituyendo
![]()
entonces
![]()
Integrando
![]()
sustituyendo (u)
![]()
___________________________
Autores:
Eduardo Ochoa Hernández
Nicolás Zamudio Hernández
Lizbeth Guadalupe Villalon Magallan
Mónica Rico Reyes
Pedro Gallegos Facio
Gerardo Sánchez Fernández
Rogelio Ochoa Barragán