La Integral
Técnica y Método
1.10. Integración por sustitución trigonométrica
Este método consiste en llevar a cabo un cambio de variable mediante funciones
trigonométricas.
Existen integrales cuyo integrando contiene expresiones de la forma:
![]()
- Integrales con la expresión:
![]()
Hacer el siguiente cambio de variable
![]()
Sustituyendo en la expresión
![]()
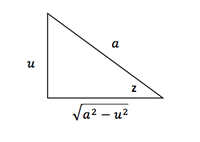
Este resultado simplificará el proceso de integración.
- Integrales con la expresión:
![]()
Hacer el siguiente cambio de variable:
![]()
Sustituyendo en la expresión
![]()
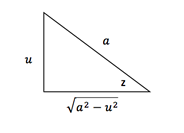
Este resultado simplificará el proceso de integración.
- Integrales con la expresión:
![]()
Hacer el siguiente cambio de variable:
![]()
Sustituyendo en la expresión
![]()
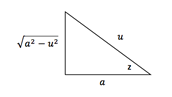
Este resultado simplificará el proceso de integración.
Veamos algunos ejemplos:
1. ![]()
El integrando contiene la expresión: ![]()
![]()
![]()
![]()
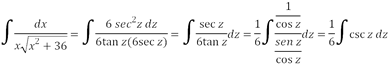
![]()
Para regresar el cambio de variable nos apoyamos con el siguiente triángulo:
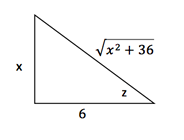
![]()
![]()
Finalmente el resultado es:
![]()
2. ![]()
El integrando contiene la expresión: ![]()
![]()
![]()
![]()
![]()
Aplicando identidad…
![]()
![]()
![]()
![]()
![]()
Para regresar el cambio de variable nos apoyamos con el siguiente triángulo:
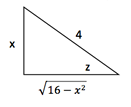
![]()
![]()
![]()
![]()
Finalmente el resultado es:
![]()
3. ![]()
El integrando contiene la expresión: ![]()
![]()
![]()
![]()
![]()
Para regresar el cambio de variable nos apoyamos con el siguiente triángulo:
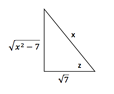
![]()
![]()
Finalmente el resultado es:
![]()
Autores:
Eduardo Ochoa Hernández
Nicolás Zamudio Hernández
Lizbeth Guadalupe Villalon Magallan
Mónica Rico Reyes
Pedro Gallegos Facio
Gerardo Sánchez Fernández
Rogelio Ochoa Barragán