

In 2025, Tiffany & Co. marks its 5-year anniversary under the ownership of luxury conglomerate LVMH. Through this period of transformation and global expansion, one visual element has remained constant: the Tiffany Blue Box. This cube-shaped box, tied with a satin white ribbon, has become a cultural icon. But behind its elegance lies geometry—specifically, the cube net.
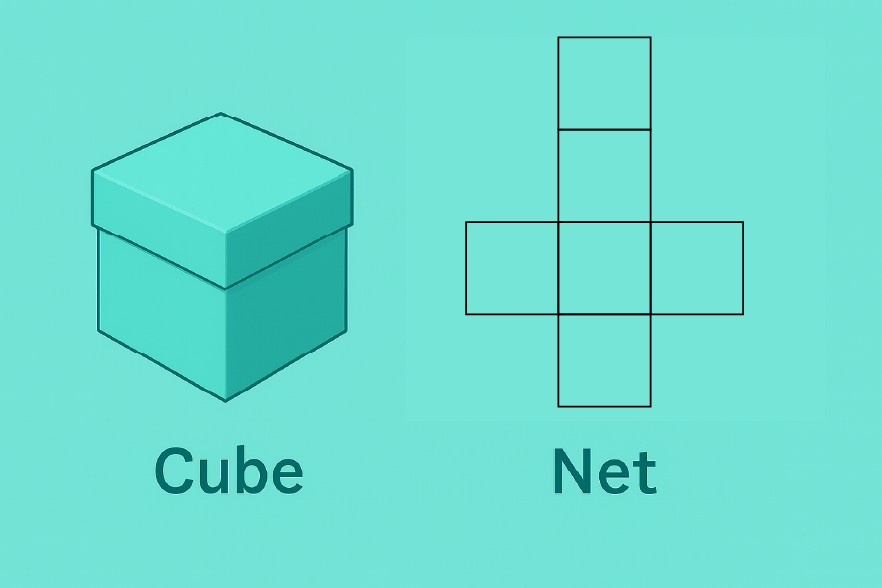
A cube net is a two-dimensional arrangement of six equal squares that, when folded, form a three-dimensional cube. Designers use this mathematical structure not only for aesthetics but also to craft memorable consumer experiences.
For a cube of side \( s \), the surface area of a cube box is calculated as \( 6s^2 \), and the volume is \( s^3 \). For example, a 10 cm cube has a surface area of 600 cm² and a volume of 1,000 cm³. Cubes evoke symmetry, balance, and quality—important for luxury branding.
The cube is one of the five Platonic solids—highly symmetrical, convex polyhedra with faces composed of identical regular polygons. Specifically, the cube consists of six square faces, twelve edges, and eight vertices. Revered since ancient times, Plato associated each solid with an element; the cube represented Earth, symbolizing stability and permanence.

These shapes fascinated Greek philosophers and mathematicians for their mathematical purity and aesthetic harmony, influencing fields from architecture to cosmology. Today, Platonic solids continue to be studied in geometry and admired for their elegant balance of form and symmetry.
Other 3D figures don't have the grandeur of cubes and other Platonic solids, but what they may lack in elegance they make up for in practicality. Mass-market goods like cereal are typically packaged in rectangular prisms. The Cheerios box, celebrating its 80th anniversary on the market, has become an iconic shape. Unlike a cube, the rectangular prism allows for better shelf fit, more space for nutritional info and branding, and greater volume-to-material efficiency.

Here is the net for a rectangular prism. Do you see the similarities and differences between this and the cube?

When you’re at the grocery store, you won’t see too many cube-shaped packages, but you will see lots of rectangular prisms. Why?

The Cheerios box—and most cereal boxes—are tall rectangular prisms for practical reasons. First and foremost, they are easier to handle and pour. Imagine holding a cube-shaped box full of cereal: it would be bulky, awkward to tip, and likely to spill. The tall, narrow shape gives your hand something to grip and helps control the flow of cereal into a bowl. Even children can pour from it without much trouble.

But this shape also turns out to be a smart marketing choice. The tall front panel acts like a mini billboard on the shelf, showing off bright colors, mascots, nutrition facts, and branding. It catches your eye. While the cube is technically more efficient in terms of packaging material, the rectangular prism wins on functionality and visual impact.
The typical size of a Cheerios cereal box is 7.5 in × 3 in × 11.5 in (length × width × height). Let's compare the volume and surface area of a Cheerios box to a cube with the same volume.
| Volume Calculation | |
Rectangular PrismVolume = length × width × height \( V = 7.5 \times 3 \times 11.5 = 258.75\ \text{in}^3 \) |
Equivalent CubeTo find the side length of a cube with the same volume: \( s = \sqrt[3]{258.75} \approx 6.37\ \text{in} \) |
A cube that has the same volume as the Cheerios box is not as tall. How do you think the surface areas compare?
| Surface Area Calculations | |
Cheerios BoxStep 1: Calculate each pair of face areas \( lw = 7.5 \times 3 \) \( lw = 22.5 \) \( lh = 7.5 \times 11.5 \) \( lh = 86.25 \) \( wh = 3 \times 11.5 \) \( wh = 34.5 \) Step 2: Add the areas \( lw + lh + wh = 22.5 + 86.25 + 34.5 \) \( lw + lh + wh = 143.25 \) Step 3: Multiply by 2 \( A = 2 \times 143.25 \) \( A = 286.5\ \text{in}^2 \) |
Equivalent CubeStep 1: Square the side length \( s = 6.37 \) \( s^2 = 6.37 \times 6.37 \) \( s^2 = 40.59 \) Step 2: Multiply by 6 \( A = 6 \times 40.59 \) \( A = 243.5\ \text{in}^2 \) |
| Container | Dimensions (in) |
Volume (in³) |
Surface Area (in²) |
S.A. / Vol. |
|---|---|---|---|---|
| Cheerios Box | 7.5 × 3 × 11.5 | 258.75 | 286.5 | 1.11 |
| Cube | 6.37 × 6.37 × 6.37 | 258.75 | 243.5 | 0.94 |
This comparison shows that although a cube uses less material for the same volume, the rectangular prism is more practical. It’s easier to grip, stack, and pour from, and offers more space for branding on the front panel.
The cube and rectangular prism aren’t the only shapes that pose design decisions. Many familiar packages make tradeoffs between efficiency, usability, shelf appeal, and manufacturing convenience. Here are a few real-world examples:

Oatmeal is often sold in cylinders, while cereal comes in rectangular boxes. Cylinders use less material for a given volume, but they don’t pack tightly on shelves or during shipping. Boxes win on storage and logistics.
Juice pouches like Capri Sun use less material and conform to their contents, but can’t stand up well, don’t reseal, and aren’t easily stackable. Juice boxes are bulkier but more user-friendly.
Some luxury products—like gourmet chocolates or holiday ornaments—are packaged in spheres. Spheres are extremely inefficient for shipping and shelving, but they draw attention and elevate the product. The geometry signals uniqueness.
Over-the-counter pills come in blister packs or bottles. Blister packs reduce misuse and increase safety, but require more plastic. Bottles are efficient and easy to use, but offer less control.
Each of these designs shows that packaging is rarely just about cost or geometry—it’s about user interaction, product protection, and emotional appeal.
We began with the cube, a symbol of elegant restraint in the Tiffany box. But geometry can go beyond minimalism. Sometimes, the shape of an object is the luxury.
Consider the Fabergé egg. This famous ovoid form doesn’t follow the logic of a package. It doesn’t maximize volume or minimize surface area. It isn’t stackable or shippable. But that’s exactly the point.
Each Fabergé egg is a handcrafted object of beauty. Its shape defies efficiency. It exists to be admired, not to be used. Geometry, in this case, becomes art.

In packaging, form usually follows function. In luxury, form is the function.
Look around your home or classroom and find 3 examples of each of the following packaging types:
Record the dimensions and think about why that shape was chosen. What does it say about the product?